The characteristic of an expression called convexity may afford some insight into the nature and reliability of a solution. Let’s consider the convexity property of a minimization problem. The mathematical definition of a convex model is as follows:

f(y) ≤ a f(x) + (1-a) f(z), where y=a*x + (1-a)*z

In words, a function is convex if, for any two points on the function, a straight line connecting the two points lies entirely on or above the function.

Determining the convexity of a multiple variable problem is no easy task. Mathematicians call a function convex if the matrix of the second derivatives is positive definite or has positive Eigen values. However, if you can identify your LINGO model as being convex for a minimization problem, you can ensure that any solution you reach is a global optimum (including nonlinear models).

A strictly convex function with no constraints has a single global minimum. Therefore, minimizing a strictly convex function will yield the unique global optimal solution regardless of the initial value of the variables. The graph below shows a convex function of a single variable:

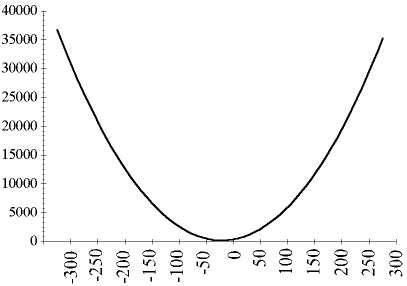
A Strictly Convex Function: Graph of .4*(X-3)2+.5

In this strictly convex function, the unique global minimum can be defined at the point on the function where the variable X is equal to 3. Changing the value of X to be more or less than 3 will increase the result of the function.

A loosely convex function with no constraints has multiple local minima, which are also global minima. Therefore, minimizing a loosely convex function may yield different solutions for different initial values of the variables. However, if you know the function is loosely convex, you will know the solution is a global minimum. For example, note the flat section (i.e., slope is zero) from approximately –200 to 150 in the following function that makes it loosely convex:

A Loosely Convex Function

In this loosely convex function, the global minimum of 3 can be found between about –200 through just over 150 on the x-axis. Although variable values may vary, the result of the function will be the same for all local minima.