Multistage Decision Making Under Uncertainty
In this chapter, the term stochastic program (SP) refers to a multistage stochastic model with recourse. The term stage is an important concept in this chapter. Usually it means the same as ‘time period’, however there are situations where a stage may consist of several time periods. The terms random, uncertain and stochastic are used interchangeably.
Multistage decision making under uncertainty involves making optimal decisions for a T-stage horizon before uncertain events (random parameters) are revealed while trying to protect against unfavorable outcomes that could be observed in the future.
| Note: | A stage boundary is either a) the beginning of the problem, b) the end of the problem, or c) a point just after a decision event but just before a random event. A stage is the sequence of random events followed by decision events between two successive stage boundaries. Thus, decisions made in stage k are based on all information revealed up to stage k, but no more. |
In its most general form, a multistage decision process with T+1 stages follows an alternating sequence of random events and decisions. Slightly more explicitly:
0.1) in stage 0, we make a decision x0, taking into account that…
1.0) at the beginning of stage 1, “Nature” takes a set of random decisions ω1, leading to realizations of all random events in stage 1, and…
1.1) at the end of stage 1, having seen nature’s decision, as well as our previous decision, we make a recourse decision x1(ω1), taking into account that …
2.0) at the beginning of stage 2, “Nature” takes a set of random decisions ω2, leading to realizations of all random events in stage-2, and…
2.1) at the end of stage 2, having seen nature’s decision, as well as our previous decisions, we make a recourse decision x2(ω1, ω2), taking into account that …
.
.
.
T.0) At the beginning of stage T, “Nature” takes a random decision, ωT, leading to realizations of all random events in stage T, and…
T.1) at the end of stage T, having seen all of nature’s T previous decisions, as well as all our previous decisions, we make the final recourse decision xT(ω1,…,ωT).
This relationship between the decision variables and realizations of random data can be illustrated as follows.
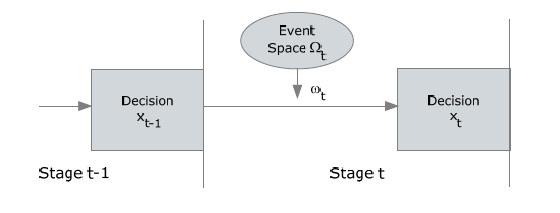
Each decision, represented with a rectangle, corresponds to an uninterrupted sequence of decisions until the next random event. And each random observation corresponds to an uninterrupted sequence of random events until the next decision point.
