A call option is a financial instrument that gives the holder the right to buy one share of a stock at a given price (the exercise price) on or before some specified expiration date. A frequent question is, "How much should one be willing to pay for such an option?" We can easily come up with some broad bounds on what we would be willing to pay.

Suppose the stock price is $105 and we have a chance to buy an option with an exercise price of $100. We should be willing to pay at least $5 for the option, because, as a minimum, we could buy the stock for $100 and immediately sell it for $105, realizing a profit of $5. Thus, when the stock price exceeds the exercise price, we should be willing to pay at least the difference in the two prices.

When the exercise price exceeds the stock price, buying at the exercise price and selling at the market price would not be an intelligent option. In this instance, the least we would be willing to "pay" would be $0.

In any case, the most we would ever be willing to pay for an option is the current price of the underlying stock. Suppose the option price was more than the stock price. Then we could get the same expected return at a lower price by buying the stock.

The following graph illustrates these bounds on an option’s value as a function of the price of the underlying stock.

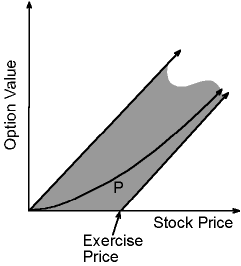
Unfortunately, these bounds are not very tight. In reality, the option value function will resemble the curve P in the graph. The exact shape of this curve is influenced by three additional factors. These are, 1) the time to expiration, 2) the volatility, or variance, in the price movements of the stock, and 3) the interest rate. The underlying formula for curve P eluded researchers for many years until Fischer Black and Myron Scholes derived it in 1973. A Nobel Prize was subsequently awarded for their work in 1997.