While convexity applies to minimization problems, concavity ensures the corresponding attribute of global optimality in maximization problems. Concavity can be defined as the negative of convexity (see above). In other words, a function is concave if, for any two points on the function, a straight line connecting the two points lies entirely on or below the function.

The following function is strictly concave:

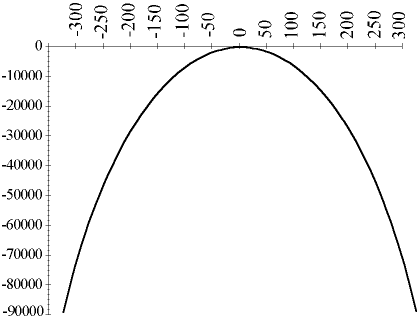
A Strictly Concave Function: Graph of -(x2)

In this strictly concave function, the unique global maximum can be defined at the point on the function where the variable x is equal to zero. Changing the value of the variable to be any more or less than 0 will decrease the result of the function

The only functions that are both convex and concave are straight lines (i.e., hyperplanes). Therefore LINGO classifies the solutions to all linear optimization problems as globally optimal. Due to the difficulty in determining convexity and concavity, LINGO classifies all nonlinear optimization models as locally optimal. However, you can ensure you have a global optimum if you can determine that your nonlinear optimization model is convex or concave, or you can reformulate it in such a way to make it convex or concave. On the other hand, if you can determine your nonlinear optimization model is definitely not convex or concave, you know that multiple optima exist and it might be a good idea to try solving with different starting values in the variables. For an example of a mixed function, see the graph of X * @COS(3.1416 *X) below.