After solving the model, you'll find that the expected value of the option is $3.37:

Local optimal solution found.

Objective value:                              3.451804

Infeasibilities:                              0.000000

Total solver iterations:                         19608

Thus, it turns out that our casual observation of the option being worthless was incorrect.  Even though the option is initially out of the money, and, on average, is expected to go even further out of the money as time passes, the option still has a positive expected value of $3.45.  This is due to the volatility in the stock price, which can temporarily send the stock price down, even though the long run expectation is for the price to climb.

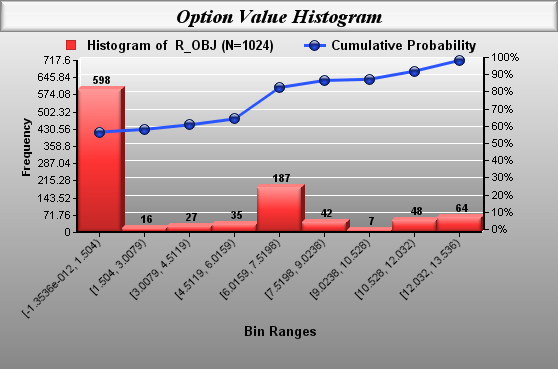
Based on our sample size of 4 in each of the 5 stages, there was a total of 1024 scenarios.  In fully 598 of these scenarios, the option's value did prove to be worthless.  However, in the remaining 426 scenarios the option had a positive value of as high as $13.54.  Here's a histogram of the full range of outcomes:

The key initial decision was whether or not to sell the option.  From the stage 0 (initial decision) solution we see that the optimal decision is to not sell:

Stage 0 Solution

----------------

         Variable           Value

        SELL( P0)        0.000000

Of course, we didn't really need LINGO to tell us not to sell in the first period - we could have deduced this ourselves.  The worst outcome we could experience is to gain $0.  By selling in the initial period, we lock in the $0 return, never allowing for the possibility of the stock to go down in price and the option to come into the money.  We will rely on LINGO's solution, however, to tell us the best time to sell in subsequent periods.  Here is a fragment of the solution report for scenario 65, which is one of the scenarios with the maximum option value of $13.54:

 Scenario: 65   Probability: 0.9765625E-03   Objective: 13.53568

 ---------------------------------------------------------------

 

    Random Variable           Value

        RETURN( P1)      -0.8000000E-01

        RETURN( P2)      -0.8000000E-01

        RETURN( P3)      -0.1000000E-01

        RETURN( P4)      -0.1000000E-01

        RETURN( P5)       0.3000000E-01

 

           Variable           Value

                 NP        6.000000

        RETURN( P0)        0.000000

         PRICE( P0)        100.0000

          SELL( P0)        0.000000

          WLTH( P0)        0.000000

         PRICE( P1)        92.00000

          SELL( P1)        0.000000

          WLTH( P1)        0.000000

         PRICE( P2)        84.64000

          SELL( P2)        1.000000

          WLTH( P2)        14.36000

         PRICE( P3)        83.79360

          SELL( P3)        0.000000

          WLTH( P3)        14.79080

         PRICE( P4)        82.95566

          SELL( P4)        0.000000

          WLTH( P4)        15.23452

         PRICE( P5)        85.44433

          SELL( P5)        0.000000

          WLTH( P5)        15.69156

Note that the stock goes down in the first four  periods, but that we sold in period 2 for a gain of $14.36, which discounted back to the initial period is equal to a gain of $13.54.  Had we been omniscient, we could have held on to the option for two more periods for additional gains.  But, of course, we can't see the future, and we must base our decisions on maximizing the option's expected value over all scenarios.