The first question to consider when building a set-based model is, "What are the relevant sets and their attributes?". In this model, we have a single primitive set, the days of the week. If we call this set DAYS, we can begin by writing our sets section as:

SETS:

  DAYS;

ENDSETS

Next, we can add a data section to initialize the set members of the DAYS set:

SETS:

  DAYS;

ENDSETS

DATA:

  DAYS = MON TUE WED THU FRI SAT SUN;

ENDDATA

Alternatively, we could use LINGO’s implicit set definition capability and express this equivalently as:

SETS:

  DAYS;

ENDSETS

DATA:

  DAYS = MON..SUN;

ENDDATA

We will be concerned with two attributes of the DAYS set. The first is the number of staff required on each day, and the second is the number of staff to start on each day. If we call these attributes REQUIRED and START, then we may add them to the sets section to get:

SETS:

  DAYS: REQUIRED, START;

ENDSETS

After defining the sets and attributes, it is useful to determine which of the attributes are data, and which are decision variables. In this model, the REQUIRED attribute is given to us and is, therefore, data. The START attribute is something we need to determine and constitutes the decision variables. Once you've identified the data in the model, you may go ahead and initialize it. We can do this by extending the data section as follows:

DATA:

  DAYS =     MON TUE WED THU FRI SAT SUN;

  REQUIRED =  20  16  13  16  19  14  12;

ENDDATA

We are now at the point where we can begin entering the model's mathematical relations (i.e., the objective and constraints). Let's begin by writing out the mathematical notation for the objective. Our objective is to minimize the total number of employees we start during the week. Using standard mathematical notation, this objective may be expressed as:

Minimize: ∑∑i STARTi

The equivalent LINGO statement is very similar. Substitute "MIN=" for "Minimize:" and "@SUM( DAYS( I):" for ∑∑i and we have:

MIN = @SUM( DAYS( I): START( I));

Now, all that is left is to come up with our constraints. There is only one set of constraints in this model. Namely, we must have enough staff on duty each day to meet or exceed staffing requirements. In words, what we want is:

Staff on duty today ≥ Staff required today, for each day of the week

The right-hand side of this expression, Staff required today, is easy to calculate. It is simply the quantity REQUIRED( I). The left-hand side, Staff on duty today, is a bit trickier to compute. Given that all employees are on a "five day on, two day off" schedule, the number of employees working today is:

Number working today = Number starting today +

Number starting 1 day ago + Number starting 2 days ago +

 Number starting 3 days ago + Number starting 4 days ago.

In other words, to compute the number of employees working today, we sum up the number of people starting today plus those starting over the previous four days. The number of employees starting five and six days back don't count because they are on their days off. So, using mathematical notation, what one might consider doing is adding the constraint:

∑∑i = j-4, j STARTi ≥ REQUIRED j , for j∈ DAYS

Translating into LINGO notation, we can write this as:

@FOR( DAYS( J):

  @SUM( DAYS( I) | I #LE# 5: START( J - I + 1))

     >= REQUIRED( J)

);

In words, the LINGO statement says, for each day of the week, the sum of the employees starting over the five day period beginning four days ago and ending today must be greater-than-or-equal-to the required number of staff for the day. This sounds correct, but there is a slight problem. If we try to solve our model with this constraint we get the error message:

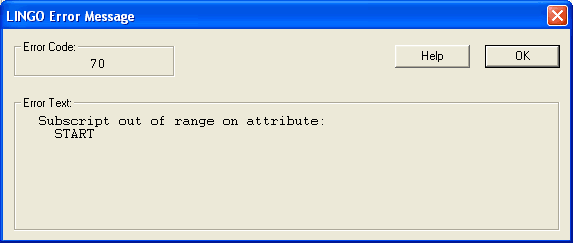
To see why we get this error message, consider what happens on Thursday. Thursday has an index of 4 in our set DAYS. As written, the staffing constraint for Thursday will be:

START( 4 - 1 + 1) + START( 4 - 2 + 1) +

START( 4 - 3 + 1) + START( 4 - 4 + 1) +

 START( 4 - 5 + 1) >= REQUIRED( 4);

Simplifying, we get:

START( 4) + START( 3) +

START( 2) + START( 1) +

 START( 0) >= REQUIRED( 4);

The START( 0) term is the root of our problem. START is defined for days 1 through 7. START( 0) does not exist. An index of 0 on START is considered "out of range."

We would like to have any indices less-than-or-equal-to 0 wrap around to the end of the week. Specifically, 0 would correspond to Sunday (7), -1 to Saturday (6), and so on. LINGO has a function that does just this: @WRAP.

The @WRAP function takes two arguments--call them INDEX and LIMIT. Formally, J = @WRAP( INDEX, LIMIT) returns J such that J = INDEX - K * LIMIT, where K is an integer such that 1 <= J < LIMIT + 1. Informally, @WRAP will subtract or add LIMIT to INDEX until it falls in the range 1 to LIMIT + 0.99999. Therefore, this is just what we need to "wrap around" an index in multiperiod planning models.

Incorporating the @WRAP function, we get the corrected, final version of our staffing constraint:

@FOR( DAYS( J):

  @SUM( DAYS( I) | I #LE# 5:

     START( @WRAP( J - I + 1, 7)))

        >= REQUIRED( J)

);