|
Faster, More Versatile Releases of LINDO API 2.0 and LINGO 8.0
LINDO Systems has recently introduced LINDO API 2.0 and LINGO 8.0. The new releases offer a number of enhancements including significantly expanded nonlinear capabilities and improved performance on linear and integer problems.
Find Better Solutions to Tough Nonlinear Problems
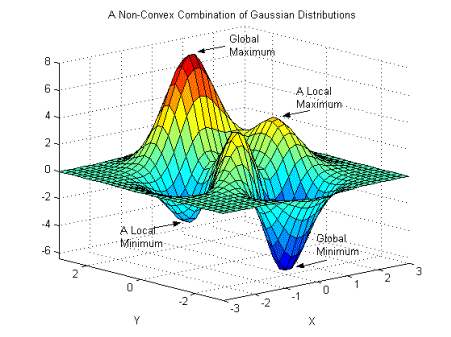
Many nonlinear models are nonconvex (e.g., they have more than one local optimum) and, as a result, not well suited to traditional solution techniques that rely on local search procedures. Local search solvers are generally designed to search only until they have identified a local optimum. If the model is non-convex, other local optima may exist that yield significantly better solutions. The new Global solver and Multistart feature included in the Nonlinear option can help find better solutions to non-convex models.
|
A Non-Convex Combination of Gaussian Distributions
 |
Determine the Proven Global Optimum
Rather than stopping after the first local optimum is found, the Global solver will search until the global optimum is confirmed. The Global solver converts the original non-convex, nonlinear problem into several convex, linear subproblems. Then, it uses the branch-and-bound technique to exhaustively search over these subproblems for the global solution.
Use Multistart to Improve Solutions
When limited time makes searching for the global optimum prohibitive, the new Multistart feature can be a powerful tool for finding good solutions more quickly. This feature intelligently generates a set of candidate starting points in the solution space. Then, the nonlinear solver intelligently selects a subset of these to initialize a series of local optimizations. For non-convex nonlinear models, the quality of the solution returned by the multistart solver will be superior to that of the general nonlinear solver.
Solve Linear and Integer Models Faster
The new releases of LINDO API and LINGO include enhancements that can significantly improve performance on many linear and integer models.
Find Faster Solutions Using the Dual Solver
The improved Dual Simplex solver in the base versions of LINDO API 2.0 and LINGO 8.0 delivers substantially better performance. On broad classes of problems, the new solver can provide speed improvements of up to 300%. The Dual Simplex solver is also even more robust due to improved handling of degenerate and numerically unstable problems.
Linearize Models Automatically
Nonlinear solvers that utilize gradient based algorithms do not perform well on models with nonsmooth functions. The new Linearization capabilities in LINDO API and LINGO can dramatically improve performance on models with common nonsmooth functions. The feature automatically converts the nonsmooth functions and operators to a series of linear, mathematically equivalent expressions. Many nonsmooth models may be entirely linearized. This allows the solver to quickly find a global solution to what would have otherwise been an intractable problem.
LINDO API can linearize the functions absolute value, if, and, or, not, max, and min as well as the operators <, <=, <>, =, >, and >=. It can also recognize and linearize the product of a binary (0/1) variable and a variable, or any product of two continuous or discrete variables constrained to be equal to, less than, or greater than zero. LINGO functions supported by linearization include @ABS(), @MAX(), @MIN(), @SMAX(), and @SMIN() along with any products of binary and continuous variables. The feature also linearizes all of LINGO's logical operators (#LE#, #EQ#, #GE#, and #NE#).
Get Quicker Solutions to Integer Problems
The new integer solver benefits from a number of enhancements that boost performance on many classes of problems. A partial list of new features includes:
 |
More advanced probing/pre-solving including lifting clique |
 |
Special pre-solving of rows with all binary variables |
 |
Additional and faster cut generation |
 |
Improved rounding heuristic |
 |
New enumeration solver for pure binary models |
 |
Many new user controllable parameters |
 |
Improved reduced cost fixing and bound tightening within the tree |
 |
Improved performance on mixed integer quadratic models |
| Â |
 |
Automatically Recognize Quadratic Models
Quadratic Programming (QP) models are a common class of nonlinear model that is encountered in financial portfolio analysis. An enhancement to LINDO API and LINGO can automatically detect if a nonlinear model has a quadratic objective and/or is quadratically constrained. If it is determined that the model is quadratic and the license includes the Barrier solver option, the solver will automatically exploit the QP structure to solve the model in a fraction of the time required by the general nonlinear solver.
Solve Decomposable Models Faster
Some large-scale linear and mixed integer problems have constraint matrices that are totally decomposable into a series of block structures. Using a new feature, the solver can detect and decompose the model, solve the independent problems sequentially, and report a solution for the original model. This results in dramatic speed improvements.
Additional Enhancements :
|
|---|
LINGO 8.0:
Solve Quadratic and Quadratically Constrained Models
-- LINGO licenses that include the Barrier option can now solve models in which the objective function and/or some constraints include quadratic terms. By taking advantage of the quadratic structure, LINGO can solve these models much more quickly than using the general nonlinear solver. LINGO can even handle quadratic models with binary and general integer restrictions. These new quadratic capabilities make LINGO suitable for applications such as portfolio optimization problems, constrained regression problems, and certain classes of difficult logistics problems (layout problems, fixed-charge-network problems with quadratic objectives).
Analyze Infeasible and Unbounded Models
-- Determining why your model is infeasible or unbounded no longer needs to be a daunting task. LINGO 8.0 includes a new set of tools that allow you to pinpoint what is causing a model to be infeasible or unbounded. The tools isolate a portion of the original model as the source of the problem. This allows you to focus your attention on a relatively small subsection of the model to look for formulation or data entry errors.
Build Multi-client and Web Applications
-- LINGO 8.0 has been re-engineered to be threadsafe for linear, integer, and quadratic models allowing one instance of the program to simultaneously work on solving multiple models. This makes LINGO 8.0 ideal for multi-client and internet applications.
LINDO API 2.0
Create Applications to Solve General Nonlinear Models
-- LINDO API is the first full-featured callable solver to offer general nonlinear and nonlinear/integer capabilities. This unique feature allows developers to incorporate a nonlinear solver into their custom applications. As with its linear and integer capabilities, LINDO API provides the user with a comprehensive set of routines for formulating, solving, and modifying nonlinear models. The Nonlinear option is required in order to utilize the nonlinear capabilities with LINDO API.
Run LINDO API from a Web Browser
-- LINDO API 2.0 includes Java Native Interface (JNI) support for Windows, Solaris, and Linux platforms. This new feature allows users to call LINDO API in applets running from a browser.
Expanded MATLAB Interface
-- The Matlab interface has been expanded to support all LINDO API functions. Using MATLAB's modeling and programming environment, you can build and solve linear, nonlinear, quadratic, and integer models and create custom algorithms based upon LINDO API's routines and solvers.
Generate the Dual Information
-- For some problem types, it can be advantageous to work with the dual formulation. LINDO API now has the ability to take a primal LP and automatically generate the dual problem.
|
|
 |
For more information on LINGO or LINDO API, please see the product pages. You can also download a demo version from our download page or order a full blown version directly from our order page.
|

